در این دنیای پرشتاب و ناپایدار، رسیدن به رشد و تعالی که لازمه آن افزایش توانمندی و بنیهی رقابتی در سازمانها است، جز با خطر کردن و تعریف اهداف استراتژیک، به نتیجه نخواهد رسید. از آنجاییکه قرارگیری در یک محیط بیثبات و نامعین، مواجهشدن با رخدادهایی خارج از برنامه میباشد، میبایست به طور مستمر و پویا، در جهت مدیریتکردن عدمقطعیتهای (رویدادهای محتمل) به وجود آمده در سازمان با بهکارگیری ابزارهایی نو و کارا، تلاش کرد.
در این راستا، لزوم استفاده از ابزارهای مدیریت ریسک، خصوصاً در محیطهای پروژهمحور به لحاظ وقوع تاخیرات زمانی و افزایش هزینهها نسبت به برآوردهای اولیه، بهشدت احساس گردیده و مدیران ارشد در سازمانها، به این واقعیت دست پیدا کردهاند که از دانش مذکور، جهت شناسایی مشکلات اینچنینی، بیشتر بهرهمند گردند و بتوانند در ساختار سازمانی خود آنها را پیادهسازی و اجرا نمایند.
بنابراین، پیادهسازی مدیریت ریسک بهعنوان یک بخش جدانشدنی در موفقیت پروژه، به شناسایی زودهنگام مشکلات احتمالی کمک کرده و از تبدیلشدن آنها به مشکلاتی در آینده، جلوگیری میکند. پیادهسازی مدیریت ریسک، همانطور که در شکل 1 نشاندادهشده، شامل شش مرحله و بهصورت یک فرآیند تکراری و مستمر در طول چرخه حیات پروژه است.
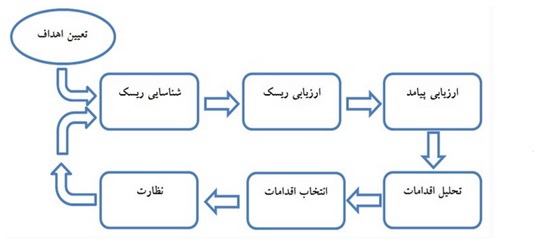
شکل 1. فرایند مدیریت ریسک
اما از آنجاکه توصیف هر کدام از مواردی که در شکل 1 نشان داده شده است، بهخودیخود بسیار مفصل است، در این مقاله صرفاً آیتم "ارزیابی ریسک" مورد بررسی قرار میگیرد و به مطالعه روشی جهت محاسبه عددی ریسکها (انتخاب شده بعد از تحلیل کیفی) میپردازد. این عدد چون متأثر از دو عامل احتمال و شدت اثر است و جهت برآورد پیچیدگیهایی را به همراه دارد، در این مقاله بررسی روشهای لازم جهت کاهش پیچیدگیهای اینچنینی مورد بحث و تحلیل قرار گرفته است تا مدیران بتوانند با محاسبه عددی ریسکهای شناسایی شده، تصویر واضحتری به تصمیمگیرندگان در جلسات ارائه نمایند.
بررسی موضوع را با پاسخ به این سوالات پیش میبریم.
- اگر پروژه در صدد محاسبه ریسک برای چند پیشآمد و رویداد به طور همزمان باشد، محاسبه "احتمال" ریسک چگونه خواهد بود؟
- عدد ریسک چه مقداری خواهد شد؟
- وقتی هدف، تحلیل عوامل تاثیرگذاری است که توأمان باعث بروز چالشهایی در خصوص تحقق زمان و هزینه در پروژه میشوند، راهکار لازم جهت پیشبینی ریسکهای مربوطه و تبدیل آنها به مقادیر Crisp (عدد واقعی)، چگونه خواهد بود؟
چنانچه مدیر پروژه در صدد محاسبه ریسک برای مدتزمان پرداخت صورتوضعیت در بخش خرید باشد، میتوان سؤالاتی ازاین قبیل را بررسی نمود.
1. احتمال پرداخت صورتحساب در کمتر از 30 روز به شرطی که میدانیم پرداختی ممکن است اتفاق نیفتد، چقدر است؟
2. درصورتیکه بدانیم پرداختی ممکن است صورت پذیرد، احتمال اینکه زمان آن کمتر از 40 روز باشد، چقدر است؟
3. ریسک آیتم شماره 1 بابت پرداخت کمتر از 30 روز چقدر است؟
4. ریسک توأم آیتم شماره 1 و 2 بابت پرداخت صورتحساب بخش خرید چقدر است؟
برای پاسخ به سؤالات فوق، از مفاهیم موجود در تئوری احتمالات استفاده گردیده و به موضوعی به نام امید ریاضی اشاره میگردد که با تعریف ریسک همخوانی داشته و کمک میکند درک بهتری از ریسک (حاصلضرب احتمال در شدت اثر رویداد) داشته باشیم.
در نتیجه اگر پروژه، در صدد محاسبه ریسک با در نظر گرفتن محاسبات احتمال با یک متغیر تصادفی باشد، ارزش انتظار (Expected Value) یا امید ریاضی وقوع تمام حالتها، جواب سؤال خواهد بود و چنانچه پیشامدهای دیگری در محققنشدن این رویدار اثرگذار باشند (تبدیل از حالت تکمتغیره به چندمتغیره و بهصورت توأم)، محاسبات ریسک، متفاوت از حالتی است که بهصورت تکمتغیره در نظر گرفته میشود و دچار پیچیدگی خواهد شد. در این مقاله هم از جنبه محاسبات مربوط بهاحتمال و هم ارزش انتظار مربوط به ریسک، به دنبال این هستیم که چگونه میتوان عدد ریسک را برای پیشآمدها بهصورت تکمتغیره و توأم که بر زمان و هزینه اتمام پروژه اثرگذار هستند، محاسبه نمود.
1. تعاریف اولیه مربوط به احتمالات
- آزمایش تصادفی، آزمایشی است که نتیجه آن از قبل معلوم نباشد؛ ولی همه نتایج ممکن آن معلوم باشد، مانند آزمایش اندازهگیری طول عمر یک لامپ که زمانهای مربوط به طول عمر لامپ که بهصورت نامتناهی از 1 ساعت تا هر مقداری که مدنظر ارزیاب باشد میتواند لحاظ گردد و یا پرتاب یک سکه که تمام حالتهای ممکن برای آن شیر یا خط میباشد؛ اما اینکه کدامیک بعد از پرتاب ظاهر میشود مشخص نیست.
- فضای نمونه آزمایش، به مجموعه نتایج ممکن در یک آزمایش گفته میشود که بهصورت همشانس (با احتمالهای یکسان) و غیر همشانس (با احتمالهای غیریکسان) قابل بسط میباشد.
- پیشامد یا رویداد (Event)، به یک زیرمجموعه از فضای نمونه آزمایش میگویند. به عنوان مثال، پیشامد ظاهرشدن 3 بار شیر در 10 بار پرتاب یک سکه یا ظاهر شدن اعداد زوج در پرتاب یک تاس و...
- احتمال (فراوانی نسبی)، به تعریفی ورای آنچه که در سطح آکادمیک و دانشگاهها انجام میشود دارد، و باید تعریفی ارائه نمود تا در دنیای واقعی کاربرد داشته و بتوان از آن در جلسات پایش پروژهها بهره برد.
در حقیقت در واقعیت ما هیچگاه فضای نمونهای همشانس برای پیشامدهای یک آزمایش تصادفی نداریم و تعاریفی که در کتابها از "احتمال" عنوان میگردد آن چیزی نیست که با آن بتوان مشکلات موجود در پروژه را حلوفصل نمود. به این دلیل که احتمال وقوع یک پیشامد A برابر است با تعداد دفعاتی از انجام آزمایش که پیشامد A رخ میدهد (n(A))، به کل تعداد دفعات انجام آزمایش (n) هرگاه شرایط انجام آزمایش یکسان باشد و تعداد دفعات انجام آزمایش به بینهایت میل کند.
این نسبت را با P(A) نشان میدهند و برای فضای نمونه غیر هم شانس برابر است با:
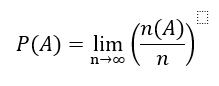 برای فضای نمونه همشانس همان فرمولی که در کتابها عنوان شده ملاک کار قرار میگیرد:
برای فضای نمونه همشانس همان فرمولی که در کتابها عنوان شده ملاک کار قرار میگیرد:
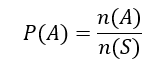 مثلاً اگر بهجای محاسبه احتمالات هر وجه از تاس، لازم باشد احتمالات وجوه یک کبریت را محاسبه کنیم، حتماً باید از فرمول فوق استفاده کنیم و بر اساس فراوانی نسبی، مقدار احتمال هر وجه از کبریت را به دست آوریم.
مثلاً اگر بهجای محاسبه احتمالات هر وجه از تاس، لازم باشد احتمالات وجوه یک کبریت را محاسبه کنیم، حتماً باید از فرمول فوق استفاده کنیم و بر اساس فراوانی نسبی، مقدار احتمال هر وجه از کبریت را به دست آوریم.
پس وقتی در "ریسک" صحبت از احتمال وقوع یک رویداد به میان میآید، منظور آزمایش یک پیشامد یا رویداد در فضای نمونه غیر همشانس بهاندازه بینهایت بار تکرار است تا بتوان با درصد خطای پایینی مقدار احتمال آن ریسک را به دست آورد. اما در واقعیت انجام بینهایت بار آزمایش، غیرممکن بوده و نمیتوان بهصورت عددی و دقیق، فراوانی نسبی رویداد یا پیشامد مدنظر را محاسبه کرد که در این صورت از روشهای شهودی (تجربه به همراه هنر)، کیفی یا غیرعددی این مقدار احتمال را در نظر میگیرند. بهعنوانمثال برای محاسبه "احتمال" در ریسک مربوط به عدم پرداخت بهموقع پول از سمت کارفرما به مدت 30 روز، میبایست تمام پیشامدهای ممکن برای پرداخت پول را بررسی نمود و فراوانی نسبی مربوط به زمان 30 روز را بهعنوان مقدار احتمال برای این ریسک لحاظ کرد که در این کیس، فضای نمونه آزمایش بهصورت غیر همشانس بوده و پس از بررسی سوابق، مشخص خواهد شد که در چه زمانهایی کارفرما پرداخت لازم را انجام داده است و متناسب با آن مقدار احتمال را محاسبه نمود. در صورت نبود سوابق میتوان با شناخت از کارفرما و تجربیات گذشته، بهصورت شهودی یا کیفی، مقدار احتمال را محاسبه نمود.
2. محاسبه احتمال مربوط به رویداد ریسک
خیلی از اوقات در دنیای واقعی به دنبال محاسبه احتمال وقوع یک رویدادی هستیم که به یکسری از رویدادها و عوامل و پیشامدهای دیگر وابسته است و به کمک قوانین ضرب احتمالات میتوان عدد احتمال را به دست آورد. به این صورت که جهت محاسبه احتمال پیشامد B در حالتی که وقوع پیشامد مذکور به پیشامدهای A1، A2، A3، … و An وابسته باشد، به کمک قانون ضرب احتمال، هر کدام از حالتها را جداگانه محاسبه کرده و در نهایت با یکدیگر جمع نماییم. به فرآیند بیان شده، "قانون احتمال کل" گفته میشود (شکل 2).
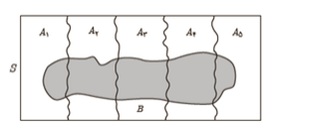
شکل 2. قانون احتمالات کل و ضرب آنها
فرض کنید رویداد پرداخت پول از سمت کارفرما مدنظر باشد و وابسته به زمانهای پرداخت پول بهصورت 50 روز، 40 روز، 30 روز، 25 روز و... گردد، احتمال این پیشامد عملاً برابر خواهد بود با:
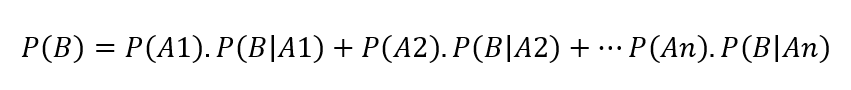 در این بخش مفهومی را که دنبال میکنیم، در شکل زیر نشاندادهشده است (شکل 3). اگر هدف محاسبه ریسک زمان مربوط به عدم پرداخت پول از سمت کارفرما باشد (بیضی قرمزرنگ)، برای محاسبه احتمال این ریسک که مقدار آن، 15% میباشد، لازم است بخشی از زمانها بهصورت پیشامدهای ناسازگار (A1…A5)، که کارفرما مطابق با آنها صورتحسابها را پرداخت کرده است، در نظر بگیریم و در نهایت احتمال وقوع رویداد عدم پرداخت پول، با استفاده از فرمول مربوط به ضرب احتمالات محاسبه شود. این موضوع بدان علت است که رویداد در نظر گرفتهشده، خود تابعی از زمانهای افرازشده (A1…A5) در فضای نمونه میباشد و میبایست بر اساس سوابق بهدستآمده از عملکرد کارفرما در پرداختهای گذشته در نظر گرفته شود.
در این بخش مفهومی را که دنبال میکنیم، در شکل زیر نشاندادهشده است (شکل 3). اگر هدف محاسبه ریسک زمان مربوط به عدم پرداخت پول از سمت کارفرما باشد (بیضی قرمزرنگ)، برای محاسبه احتمال این ریسک که مقدار آن، 15% میباشد، لازم است بخشی از زمانها بهصورت پیشامدهای ناسازگار (A1…A5)، که کارفرما مطابق با آنها صورتحسابها را پرداخت کرده است، در نظر بگیریم و در نهایت احتمال وقوع رویداد عدم پرداخت پول، با استفاده از فرمول مربوط به ضرب احتمالات محاسبه شود. این موضوع بدان علت است که رویداد در نظر گرفتهشده، خود تابعی از زمانهای افرازشده (A1…A5) در فضای نمونه میباشد و میبایست بر اساس سوابق بهدستآمده از عملکرد کارفرما در پرداختهای گذشته در نظر گرفته شود.
درحقیقت چندین عامل در محاسبه این احتمال اثرگذار بودند که اگر در نظر گرفته نشوند، در حقیقت مقدار احتمال مربوطه فاقد حدود درستی بوده و در نهایت محاسبه عدد ریسک واقعی نخواهد بود.
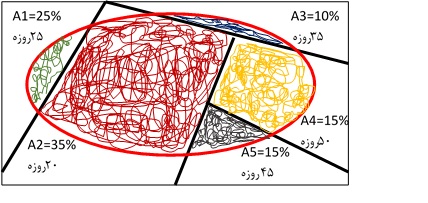
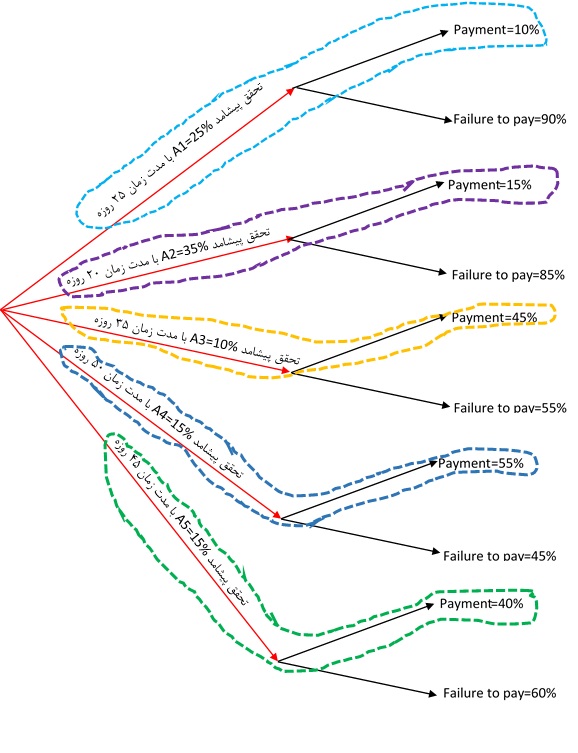
شکل 4. نمودار درختی مربوط به محاسبه احتمال پیشامد B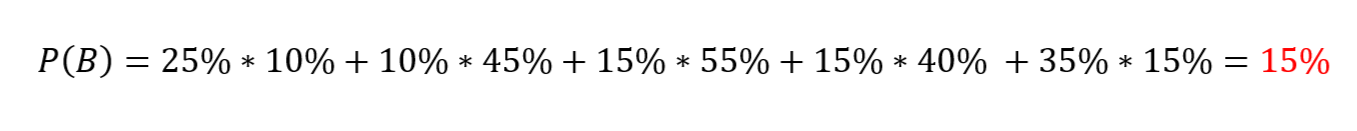 جهت شفافتر شدن موضوع میتوان از شکل 4، برای نشاندادن محاسبات احتمال استفاده کرد:
جهت شفافتر شدن موضوع میتوان از شکل 4، برای نشاندادن محاسبات احتمال استفاده کرد:
3. بررسی رویدادهای همزمان
سوال این است که در مثال قبل، مقدار ریسک باتوجه به مقدار احتمال مربوطه (15%)، چقدر است؟ برای پاسخ میبایست تعریفی از ریسک بر اساس مفهوم امید ریاضی (Expected Value) به این بیان داشت: صورت که امید ریاضی، میانگین بینهایت نتایج تکرار یک آزمایش بوده که به آن ارزش انتظار یا میانگین وزنی هم اطلاق میگردد. مثلاً در بینهایت پرتاب یک تاس، میانگین اعداد ظاهر شده برابر است با عدد 3.5، به این شکل که اگر تاس را بینهایت بار، مثلاً یک میلیون بار، پرتاب کنند، میانگین و متوسط عددی که ظاهر میشود 3.5 خواهد بود که بهصورت زیر نشان داده میشود:
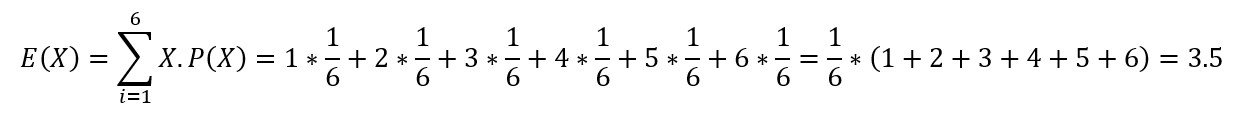
ریسک تعاریف متنوعی دارد. میتوان گفت که ریسک:
- یک رویداد یا مجموعهای از رویدادهای محتمل که در صورت وقوع، بر دستیابی اهداف تأثیر میگذارد.
- احتمال وقوع یک رویداد که در صورت محققشدن، شدت اثر لازم را بر دستیابی اهداف تعریفشده خواهد گذاشت.
- شکلی ترکیبی از احتمال وقوع یک تهدید یا فرصت است که میزان تأثیر آن بر اهداف اندازهگیری میشود.
لذا اگر X (متغیر تصادفی) را در فرمول امید ریاضی، شدت اثر و P(X) را مقدار احتمال ریسک در نظر بگیریم، تعریفی که برای امید ریاضی مطرح شد، میتواند برای ریسک استفاده گردد. مثلاً چنانچه بخواهیم بدانیم در 5 بار پرتاب یک سکه، ریسک آمدن تعداد شیر چقدر خواهد بود، از روش زیر باید عمل کنیم؟
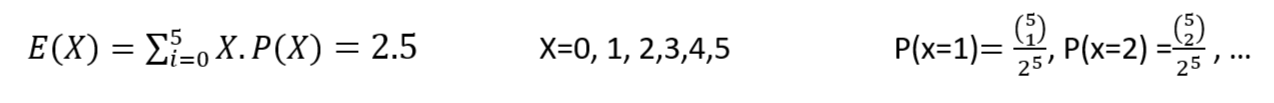
ولی در این حالت متغیر تصادفی X، تکمتغیره بوده و میتواند بهصورت چندمتغیره مورد بررسی قرار گیرد. به این صورت که اگر هدف پیداکردن ریسک زمان پرداخت پول از سمت کارفرما باشد، صرفاً نمیتوان فقط عامل زمان پرداخت را ملاک عمل قرارداد و بایستی ترکیبی از موضوعات دیگر مانند آمادهبودن مدارک در زمان مقرر، دریافت بهموقع تأییدیه از کارفرما جهت ارسال صورتحساب و... را هم مدنظر قرارداد تا ریسک عدم پرداخت بهموقع پول توسط کارفرما عددی قابلاتکا برای تصمیمگیری باشد. لذا امید ریاضی از حالت بررسی تکمتغیره، تبدیل به امید ریاضی توأم میگردد و محاسبات ریسک میتواند بر اساس اثرگذار بودن چند عامل به طور همزمان محاسبه گردد.
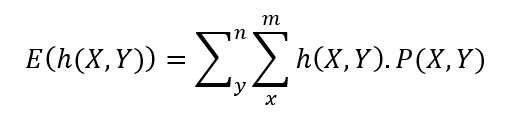 در رابطه مذکور h(X,Y)=Z میتواند بهصورت ترکیبی از مقادیر رویدادهای مدنظر باشد
در رابطه مذکور h(X,Y)=Z میتواند بهصورت ترکیبی از مقادیر رویدادهای مدنظر باشد
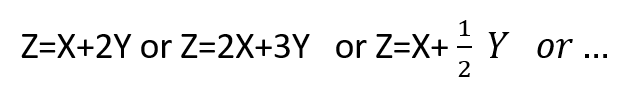
فرض کنید اگر گروهی تحقیقکننده به دنبال محاسبه ریسک یک رویداد باشند که رویداد مذکور بیانکننده سالمبودن یا نبودن افراد یک جامعه بر اساس نمونهگیری از یک جامعه (نامتناهی) میباشد، عملاً رویدادهایی مثل بررسی فشار خون، میزان تپش قلب، میزان دیابت و میزان چربی خون، میتواند بهعنوان عوامل تاثیرگذار در مشخصشدن ناخوشاحوال بودن افراد نمونهگیریشده از جامعه لحاظ گردند؛ لذا اگر عدد ریسک محاسبه شده، بالای 15 بود، تشخیص به عدم سلامتی و اگر بین 10 تا 15 بود، تقریباً نرمال و چنانچه پایینتر از 10 بود، دلیل بر سالمبودن فرد انتخابشده در نظر گرفته خواهد شد. اگر چهار عامل فوق بهعنوان شاخصی برای بررسی هدف انتخابشده لحاظ گردیده باشند، عملاً مقدار عددی ریسک رویداد سالمبودن تابعی از این چهار رویداد در هر بار نمونهگیری میباشد که در وهله اول میبایست مقدار احتمال هر یک از این 4 رویداد را به طور نظری، شهودی یا نظریه احتمالات و ... محاسبه نمود.
بهعنوانمثال برای محاسبه احتمال داشتن فشار خون به مقدار 15%، بدین صورت عمل میگردد که 5 پیشامد در نظر گرفته و فراوانی نسبی پنج پیشامد محاسبه شده و نهایتاً افرازی از این پیشامدها با عنوان پیشامد دارا بودن فشار خون، اعمال (پیشامد بیضی قرمزرنگ) و احتمال آن طبق فرمول زیر محاسبه میگردد، چرا که داشتن فشار خون خود تابعی از سایر عوامل دیگر میباشد که در شکل زیر نمایشدادهشده است:
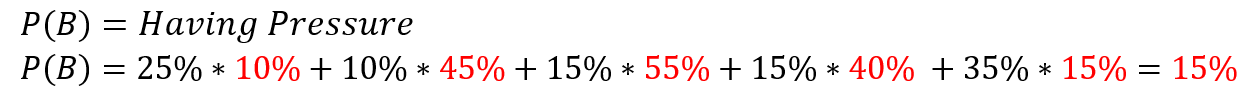
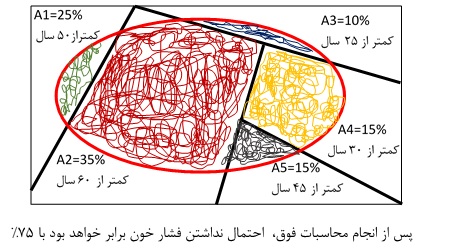 شکل 5. محاسبه احتمال یک پیشامد در رویدادهای توام
شکل 5. محاسبه احتمال یک پیشامد در رویدادهای توام
و به همین صورت برای مابقی عوامل و رویدادهای تعریف شده، احتمالات را محاسبه نموده و درنهایت عدد ریسک را بر اساس ارزش انتظار برای تکمتغیر، در صورت داشتن فشار خون با احتمال 15% و مقداری برابر با 10، دیابت با احتمال 20% و مقداری برابر با 15، چربی خون با احتمال 12% و مقداری برابر با 18، تپش قلب با احتمال 15% و مقداری برابر با 20 به دست میآوریم که برابر خواهد بود با:
E(X) = 15%* 10+20%*15+12%*18+15%*20=10
که عدد بهدستآمده نشان از عدم ناخوشاحوال بودن فرد میدهد. چنانچه لازم باشد، مقدار ارزش انتظار بر اساس تأثیر سایر عوامل به طور همزمان محاسبه میگردد و میبایست مقادیر احتمال بر اساس پیشامدی که شامل تمام عوامل (فشار خون، دیابت، چربی خون و تپش قلب) میباشد محاسبه گردد و عملاً نمونه انتخابشده بهصورت حاصل جمع کل مقادیر مشاهدهشده و مطابق با فراوانی نسبی آنها، در نظر گرفته و احتمال مربوطه محاسبه گردد (اعداد در یک بازه بین 0 تا 20 در نظر گرفته شده اند).
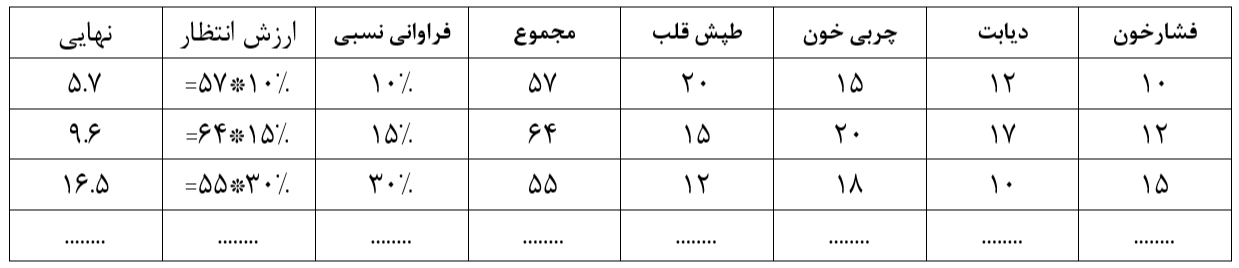
جمعبندی محاسبات کمی ریسک برای یک یا چند رویداد همزمان
استفاده از مفاهیم و کاربرد آمار و احتمالات در جهت مدیریت عدمقطعیتها، میتواند بسیار کارساز بوده و برای تصمیمات مدیران پروژه در حین اجرا کمککننده باشد. با استفاده از این مفاهیم، مدیران پروژه، در جلسات مدیریتی، بهترین روشهای حل مسئله جهت برونرفت از محققنشدن اهداف پروژه (تحقق زمان و هزینه در بازه مشخص) جهت اتخاذ تصمیمات آنی و درستتر را بررسی نموده و به کار میگیرند. در نتیجه محاسبه درست احتمال با درنظر گرفتن وابستگی موجود بین پیشامدهای دیگر (افرازی از پیشامدها) و اثرگذار بودن آنها نسبت به یکدیگر، برای رسیدن به ریسکهای شناسایی و انتخاب شده در پروژهها، بسیار حائز اهمیت بوده و باعث میگردد مدیریت در گرفتن تصمیمات مهم مرتبط با اهداف قرارداد شده، درصد خطای کمتری داشته باشد. چون هر رویداد و پیشامد، تابعی از تهدیدها و فرصتهاست، میبایست برای محاسبه ریسک، ترکیبی از پیشامدهای با علامت مثبت و منفی را دخیل نمود تا عدد ریسک در یک بازه خوشبینانه و بدبینانه باشد و بتواند در اختیار پروژه و ذینفعان مربوطه قرار بگیرد.






















عاطفه قرباغی
2 سال پیش
بسیار عالی
پاسخپشتیبان
2 سال پیش
از محبتتون سپاسگزاریم
پاسخ